ТУННЕЛЬНЫЙ ЭФФЕКТ, квантовый эффект, состоящий в проникновении квантовой частицы сквозь область пространства, в к-рой согласно законам классич. физики нахождение частицы запрещено. Классич. частица, обладающая полной энергией E и находящаяся в потенц. поле, может пребывать лишь в тех областях пространства, в к-рых ее полная энергия не превышает потенц. энергию U взаимодействия с полем. Поскольку волновая ф-ция квантовой частицы отлична от нуля во всем пространстве и вероятность нахождения частицы в определенной области пространства задается квадратом модуля волновой ф-ции, то и в запрещенных (с точки зрения классич. механики) областях волновая ф-ция отлична от нуля.

T. э. удобно иллюстрировать на модельной задаче об одномерной частице в поле потенциала U(x) (x - координата частицы). В случае симметричного двухъямного потенциала (рис. а)волновая ф-ция должна "умещаться" внутри ям, т. е. она представляет собой стоячую волну. Дискретные энерге-тич. уровни, к-рые расположены ниже барьера, разделяющего минимумы потенциала, образуют близко расположенные (почти вырожденные) пары. Разность энергетич. уровней, составляющих пару, наз. туннельным расщеплени-е м, эта разность обусловлена тем, что точное решение задачи (волновая ф-ция) для каждого из квантовых состояний дело-кализовано в обоих минимумах потенциала и все точные решения отвечают невырожденным уровням (см. Вырождение энергетических уровней). Вероятность T. э. определяется коэффициентом прохождения сквозь барьер волнового пакета, к-рый описывает нестационарное состояние частицы, локализованной в одном из минимумов потенциала.

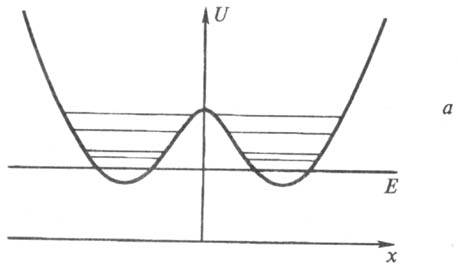
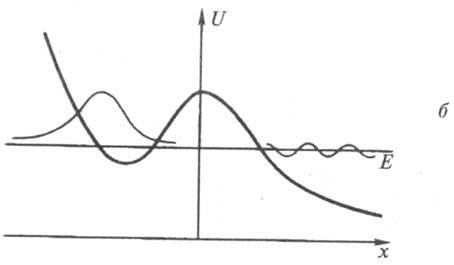
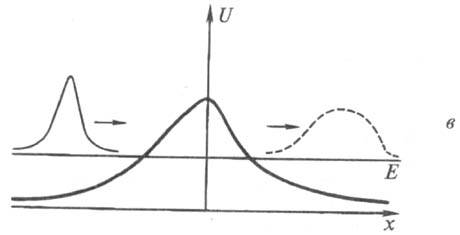
Кривые потенц. энергии U (х)частицы в случае, когда на нее действует сила притяжения (а - две потенц. ямы, б - одна потенц. яма), и в случае, когда на частицу действует сила отталкивания (отталкивательный потенциал, в). E -полная энергия частицы, х - координата. Тонкими линиями изображены волновые ф-ции.

В потенц. поле с одним локальным минимумом (рис. б)для частицы с энергией E, большей потенциала взаимодействия при c =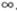, дискретные энергетич. состояния отсутствуют, но существует набор квазистационарных состояний, в к-рых велика относит. вероятность нахождения частицы вблизи минимума. Волновые пакеты, отвечающие таким квазистационарным состояниям, описывают метастабильные квантовые состояния; волновые пакеты расплываются и исчезают вслед-ствии T. э. Эти состояния характеризуются временем жизни (вероятностью распада) и шириной энергетич. уровня.

Для частицы в отталкивательном потенциале (рис. в)волновой пакет, описывающий нестационарное состояние по одну сторону от потенц. барьера, даже если энергия частицы в этом состоянии меньше высоты барьера, может с определенной вероятностью (наз. вероятностью проникновения или вероятностью туннелирования) проходить по др. сторону барьера.

Наиб. важные для химии проявления T. э.: 1) туннельные расщепления дискретных колебат., вращат. и электронно-ко-лебат. уровней. Расщепления колебат. уровней в молекулах с неск. эквивалентными равновесными ядерными конфигурациями - это инверсионное удвоение (в молекулах типа аммиака), расщепление уровней в молекулах с заторможенным внутр. вращением (этан, толуол) или в нежестких молекулах, для к-рых допустимы внутримол. перегруппировки, приводящие к эквивалентным равновесным конфигурациям (напр., PF₅). Если разл. эквивалентные минимумы на поверхности потенциальной энергии оказываются разделенными потенц. барьерами (напр., равновесные конфигурации для право- и левовращающих изомеров сложных молекул), то адекватное · описание реальных мол. систем достигается с помощью, локализованных волновых пакетов. В этом случае пара дело-кализованных в двух минимумах стационарных состояний неустойчива: под действием очень малых возмущений возможно образование двух состояний, локализованных в том или ином минимуме.

Расщепление квазивырожденных групп вращат. состояний (т. наз. вращательных к л а с т е r о в) также обусловлено туннелированием мол. системы между окрестностями неск. эквивалентных стационарных осей вращения. Расщепление электронно-колебат. (вибронных) состояний происходит в случае сильных Яна - Теллера эффектов. С туннельным расщеплением связано и существование зон, образуемых электронными состояниями отдельных атомов или мол. фрагментов в твердых телах с периодич. структурой.

2) Явления переноса частиц и элементарных возбуждений. Данная совокупность явлений включает нестационарные процессы, описывающие переходы между дискретными состояниями и распад квазистационарных состояний. Переходы между дискретными состояниями с волновыми ф-циями, локализованными в разл. минимумах одного адиабатич. потенциала, соответствуют разнообразным хим. р-циям. T. э. всегда вносит нек-рый вклад в скорость р-ции, однако этот вклад существен только при низких т-рах, когда надбарьер-ный переход из исходного состояния в конечное маловероятен из-за низкой заселенности соответствующих уровней энергии. T. э. проявляется в неаррениусовском поведении скорости r-ции; характерный пример - рост цепи при ради-ационно-инициированной полимеризации твердого формальдегида. Скорость этого процесса при т-ре ок. 140 К удовлетворительно описывается законом Аррениуса с энергией активации 0,1 эВ. Однако при т-рах 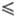12 К достигается скорость р-ции, к-рая не зависит от т-ры, определяется T. э. и оказывается на много порядков выше скорости, к-рую можно было бы ожидать при той же т-ре в предположении справедливости надбарьерного механизма р-ции (см. Криохимия).

Распад метастабильных состояний лежит в основе целого ряда явлений. К ним относятся, в частности, ос-распад (см. Радиоактивность), колебат. и вращат. предиссоциациА, автоионизация атомов в сильном электрич. поле, ионизация атомов и молекул в сильном электромагн. поле. Туннельное прохождение электронов из одного проводника (или полупроводника) в другой через слой изолятора (туннельный ток) является макроскопич. эффектом, обусловленным T. э. Это явление лежит в основе туннельной сканирующей микроскопии твердых тел.

===
Исп. литература для статьи «ТУННЕЛЬНЫЙ ЭФФЕКТ»: Гольданский В.И., Трахтенб ерг Л.И., Флеров В.П., Туннельные явления в химической физике, M., 1986; Ландау Л. Д., Лиф-шиц E. M., Квантовая механика. Нерелятивистская теория, 4 изд., M., 1989.

Б.И. Жилинский.

Страница «ТУННЕЛЬНЫЙ ЭФФЕКТ» подготовлена по материалам химической энциклопедии.